
SmoothL1Lossは損失関数の一つで、L1Loss類似しており、同様に回帰問題に対してよく使われる損失関数ではありますが、勾配爆発を防ぎつつ、学習が安定する損失関数の一つとしてよく使われます。今日はSmoothL1Lossについて解説していきます。
そもそも損失関数とは?
深層学習、いわゆるDNN(ディープニューラルネットワーク)おいて損失関数は、そのネットワークにおける予測値と正解値をパラメータとして持ち、そのネットワークを評価するための指標として使われます。DNNを学習させるということは、損失関数を最小化するようにネットワークのパラメータ(重み)を更新することであり、損失関数の値を元にパラメータの更新が行われます。この損失関数の値が大きい場合には、その値が小さくなるように勾配法を用いて、ネットワークパラメータを更新します。
厳密には、評価指標(検出率や、検出精度、認識精度)などとは別であり、あくまでネットワーク単体における評価を損失関数を用いて行い、その値を使ってDNNのパラメータを更新することになります。
L1Lossとは?
SmoothL1Lossと似ているL1Lossとはそもそも何でしょうか?よくMAE(MeanAbsoluteError)としても知られ、いわゆる平均絶対誤差と日本語では言われています。真値(学習で用いる正解値)と実際のモデルの予測値の差の絶対値を取り平均をとったものになります。
数式で表すと以下のようになります。
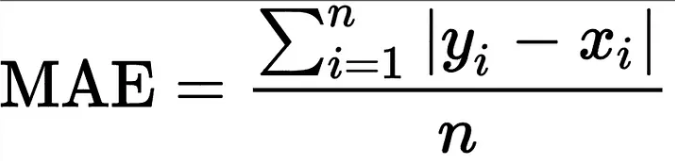
yiが予測値、xiが真値を表します。nが対象数になるので、差の絶対値の和を取ってnで割り平均を出しているのが、直感的にもわかると思います。非常にシンプルな損失関数ではありますが、「正解値との差」というシンプルかつ直感的であるため、現在でも広く使われている損失関数の一つになります。
SmoothL1Lossとは?
SmoothL1Lossにおける計算式は以下になります。

βはハイパーパラメータであり、このβは外れ値に基づいて決定することが望ましいですが、Pytorchでも多くの場合でもデフォルトとして1.0が設定されています。推論値と正解値の差がβ以下の場合、損失関数の計算はMSEライクな計算になり、それ以外の場合はMAEライクな計算になります。ラフにまとめると以下のような性質となります。
- 損失関数が小さい値をとる場合には、2次関数のように滑らかに0に漸近するような関数となる
- 損失関数が大きい値をとる場合には、1次関数のように線形な増減をする関数となる
つまりSmoothL1Lossは0に近いところも、それ以外のところも滑らかに変化する損失関数ということになります。
SmoothL1Lossを用いるメリットは何なのか?
それでは、L1Lossの代わりにSmoothL1Lossを用いるメリットは何なのでしょうか?SmoothL1LossのほうがL1Lossよりも学習が安定するといわれています。その理由としては、主に以下が挙げられます。
- 誤差が0に近い付近で学習が安定しなくなる
- 外れ値に関する感度が高い
誤差が0に近い付近で学習が安定しなくなる
L1Lossの場合、誤差が0になると勾配消失が起こり、微分が不可能になる点や、0に近い付近でも大きな勾配を取ってしまうという欠点があります。
外れ値に対する感度が高い
MSE(平均二乗誤差)ほどではないですが、L1Lossも外れ値に対する感度がSmoothL1Lossよりも高くなります。そうすると外れ値が発生した際に収束がしにくくなります。
以下のグラフは参考サイトから引用してきた、L1LossとSmoothL1Lossの比較を行ったものになります。同じ真値と同じ予測値を持たせたときの損失関数の値を比べているのですが、損失が0に近いx=40の付近では、L1よりもSmoothL1のほうが滑らかに収束していっているのがわかります。また真値と予測値の差が大きくなるにつれて、L1Lossのほうが大きな値を取ってしまっていることがわかると思います。これのように誤差に対する感度が高いと勾配爆発と呼ばれる現象が発生し、学習が安定しなくなってしまいます。
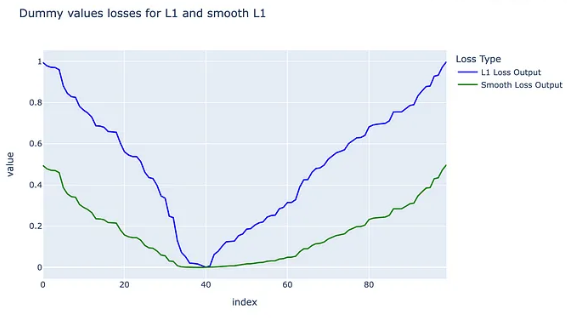
これらの点から、SmoothL1Lossを用いる方が、学習が安定するといわれています。
まとめ
SmoothL1Lossについて解説し、L1Loss1と比べてなぜ学習が安定するのかについて解説しました。学習時の参考になれば幸いです。
参考リンク
medium: https://someshfengde.medium.com/understanding-l1-and-smoothl1loss-f5af0f801c71